The objective of this blog post is to provide a detailed understanding of how numerical operations in Solidity can encounter precision loss if they are not handled properly. This is an addition to the series from our earlier blog, where we shared the details of Integer Overflow and Underflow, Front Running Attack, Understanding Block Timestamp Manipulation, and Issues with Authorization Using tx.origin.
Introduction#
Solidity compilers above version 0.4.24 don't support floating-point or fixed-point data types. Floating point numbers represent decimal numbers as a binary fraction and can result in precision loss during calculations. This means that the design of smart contracts requires careful consideration of how numbers are handled, especially in the case of floating points. The loss of precision can cause a serious threat, which can lead to unintended or potentially catastrophic consequences for smart contract functionalities.
Vulnerability#
Solidity uses a fixed-point number system, where the data type and the number of decimal places are predetermined. During an arithmetic operation involving floating-point numbers, the result of the code execution may not be accurate due to the limited precision of the fixed-point system. These can cause unexpected behavior in the smart contract functionality, such as rounding errors or arithmetic overflow and underflow conditions that can manifest itself through a huge loss of funds.
Consider a smart contract that distributes payments to individuals based on a share-wise percentage split. If this contract uses floating-point numbers for calculations, there is a risk of precision loss if those calculations are not handled properly. This could result in the funds to be paid being lost during the payment process, or not being distributed as intended causing serious financial implications.
In yet another case, consider a smart contract that is intended for gambling or playing games. If the contract makes use of floating-point numbers to calculate the payout or probabilities of individual distribution, a loss of precision can favor one party over another. This can lead to unfairness in reward distribution, resulting in the individual's loss of funds, or potentially a legal action against the host.
Attack Scenario#
Consider the below smart contract ArithmeticOp.sol,
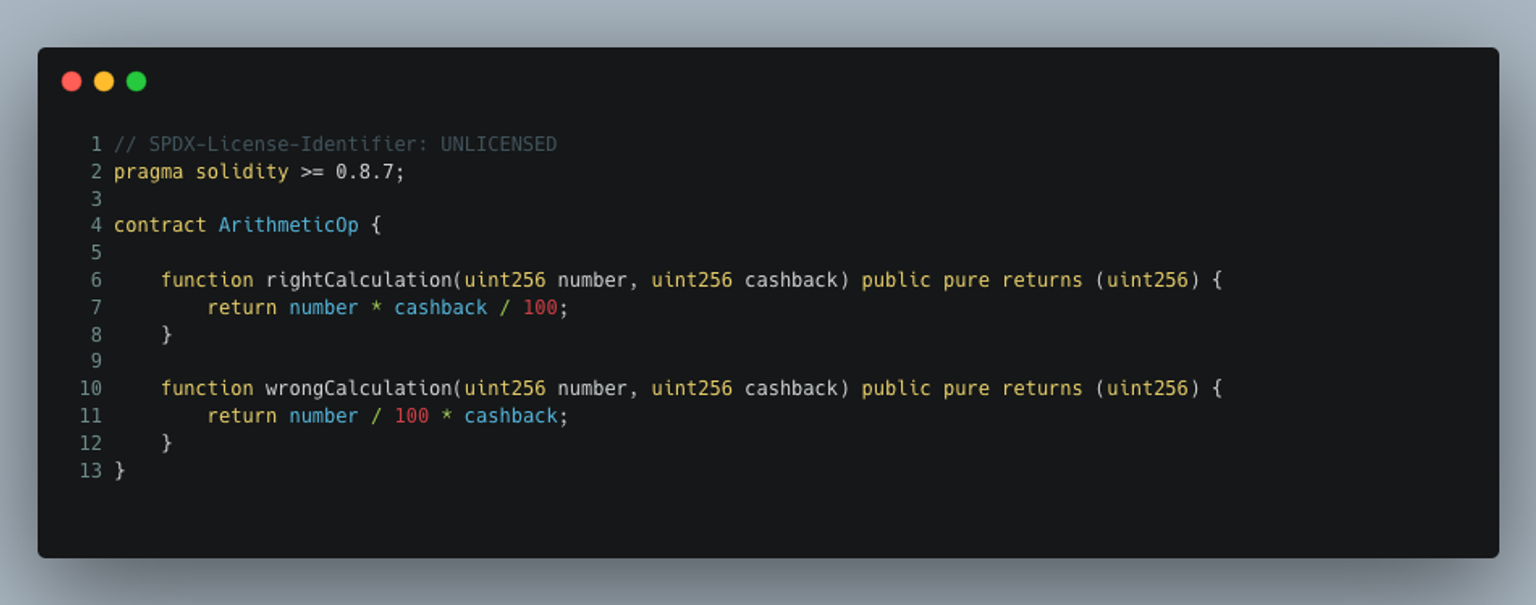
This contract includes two functions: rightCalculation, and wrongCalculation, both with parameters number, and cashback. These functions take in a number, computes a calculation for a cashback, and returns the cashback value when a given number is submitted.
On line 7 of the contract and inside the rightCalculation function, the return value is calculated in such a way that the multiplication operation precedes the division operation.
On the other hand in line 11 inside the wrongCalculation function, the return value is calculated in such a way that the division operation precedes the multiplication operation.
Attack Explained#
Let us test this smart contract by generating a sample test case as described in the below image.
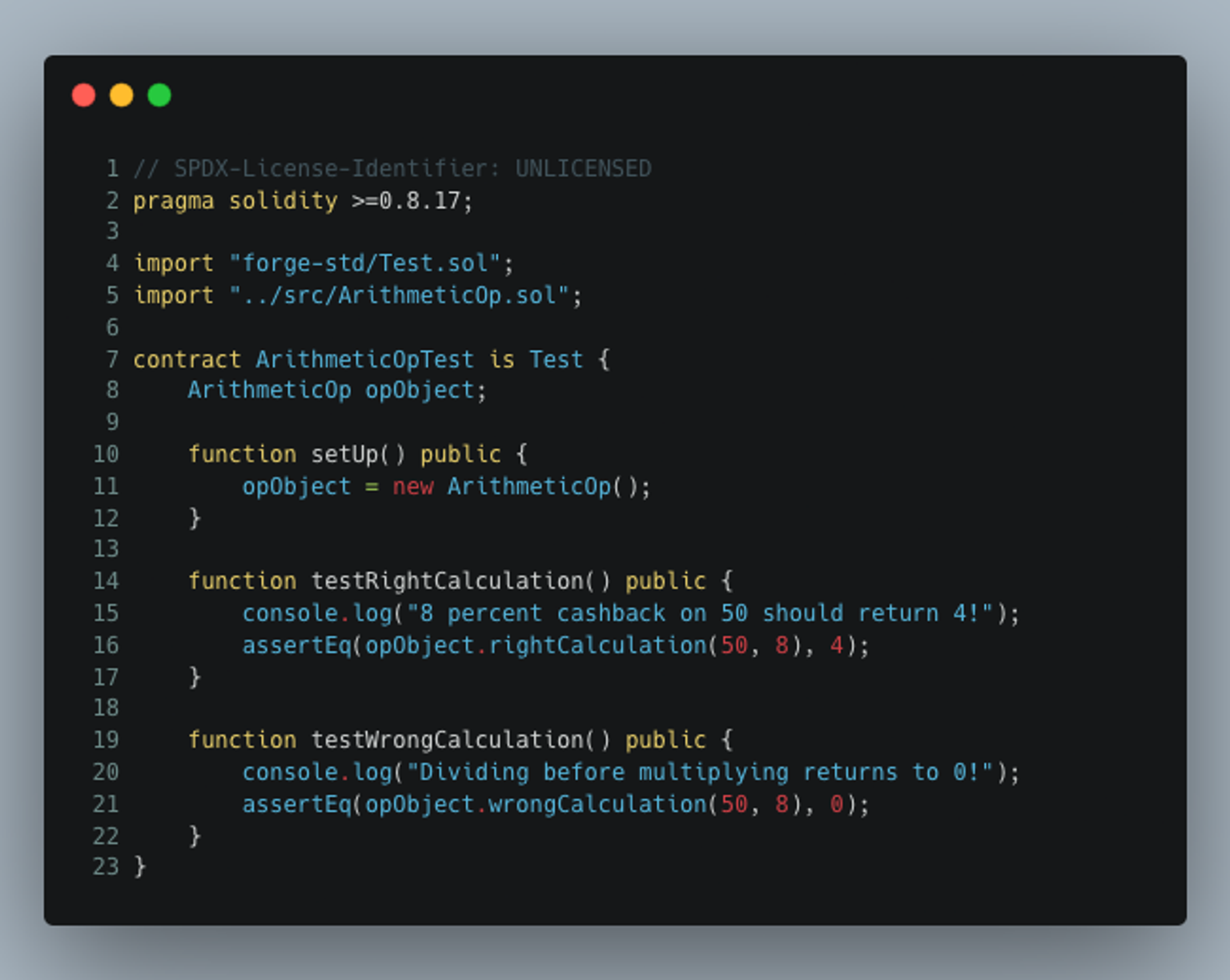
The function on line 14 on this contract is intended to test the rightCalculation function from the ArithmeticOp contract. The rightCalculation function is called using parameters ‘number’ as 50, and ‘cashback’ as 8. As the multiplication operation precedes the division operation, the result of this operation is returned as 4. (50 * 8 / 100 → 400 / 100 → 4).
However, the function on line 19 on this contract is intended to test the wrongCalculation function from the ArithmeticOp contract. The wrongCalculation function is called using parameters ‘number’ as 50, and ‘cashback’ as 8. As the division operation precedes the multiplication operation, the result of this operation is returned as 0, because the ‘uint256’ variable isn’t able to handle the floating point number as a result of the division first operation. (50 / 100 * 8 → 0.5 * 8 → 0). Therefore, the two same functions with same functional parameters, but with different order of operations resulted in two different outputs.
Prevention#
It is important to keep the right precision in numerical operations, especially when dealing with calculations that involve ratios, rates, percentages, or other economic decisions. All of these numbers should allow for larger numerators in fractions.
It is also important to be mindful about the order of operations. If a calculation requires the use of both multiplication and division operations at once, then the multiplication operation should always be performed before the division operation. It is also recommended to convert variables into higher precision, perform all mathematical operations, and then finally convert them back to the needed precision wherever necessary.
Conclusion#
It is crucial to be careful of precision loss or rounding errors when executing mathematical operations on Solidity, which can occur because a fixed amount of memory can only hold a certain number of digits.Thus, it is important to carefully design the smart contract functionalities to avoid any precision loss during their computation.
